ARTÍCULOS ORIGINALES

Meta-análisis para evaluar eficiencia de selección genómica en cereales

Meta-analysis for evaluating the efficiency of genomic selection in cereals

 

Rueda Calderón M. A.^1,2 , Balzarini M.^1,2, Bruno C.^1,2*

¹ Estadística y Biometría. Facultad de Ciencias Agropecuarias. Universidad Nacional de Córdoba, Córdoba, Argentina. Ing. Agr. Félix Aldo Marrone 746. Ciudad Universitaria, Córdoba, Argentina
² Unidad de Fitopatología y Modelización Agrícola (UFyMA), Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Córdoba, Argentina.
Corresponding author: Cecilia Bruno cebruno@agro.unc.edu.ar

DOI: 10.35407/bag.2020.31.01.03

Received: 03/09/2020
Revised version received: 04/23/2020
Accepted: 04/28/2020

---

RESUMEN

La selección genómica (SG) es usada para predecir el mérito de un genotipo respecto a un carácter cuantitativo a partir de datos moleculares o genómicos. Estadísticamente, la SG requiere ajustar un modelo de regresión con múltiples variables predictoras asociadas a los estados de los marcadores moleculares (MM). El modelo se calibra en una población en la que hay datos fenotípicos y genómicos. La abundancia y la correlación de la información de los MM dificultan la estimación, y por ello existen distintas estrategias para el ajuste del modelo basadas en: mejor predictor lineal insesgado (BLUP), regresiones Bayesianas y aprendizaje automático. La correlación entre el fenotipo observado y el mérito genético predicho por el modelo ajustado, provee una medida de eficiencia (capacidad predictiva) de la SG. El objetivo de este trabajo fue realizar un meta-análisis de la eficiencia de la SG en cereales. Se realizó una revisión sistemática de estudios relacionados a SG y se llevó a cabo un meta-análisis, para obtener una medida global de la eficiencia de la SG en trigo y maíz, bajo diferentes escenarios (cantidad de MM y método estadístico usado para la SG). El metaanálisis indicó un coeficiente de correlación promedio de 0,61 entre los méritos genéticos predichos y los fenotipos observados. No se observaron diferencias significativas en la eficiencia de la SG realizada con modelos basados en BLUP (RR-BLUP y GBLUP), enfoque estadístico más comúnmente usado. El incremento de MM no cambia significativamente la eficiencia de la SG.

Palabras clave: Revisión sistemática; Modelos de efectos aleatorios; Forest plot; Capacidad predictiva.

ABSTRACT

Genomic selection (GS) is used to predict the merit of a genotype with respect to a quantitative trait from molecular or genomic data. Statistically, GS requires fitting a regression model with multiple predictors associated with the molecular markers (MM) states. The model is calibrated in a population with phenotypic and genomic data. The abundance and correlation of MM information make model estimation challenging. For that reason there are diverse strategies to adjust the model: based on best linear unbiased predictors (BLUP), Bayesian regressions and machine learning methods. The correlation between the observed phenotype and the predicted genetic merit by the fitted model provides a measure of the efficiency (predictive ability) of the GS. The objective of this work was to perform a metaanalysis on the efficiency of GS in cereals. A systematic review of related GS studies and a meta-analysis, in wheat and maize, was carried out to obtain a global measure of GS efficiency under different scenarios (MM quantity and statistical models used in GS). The meta-analysis indicated an average correlation coefficient of 0.61 between observed and predicted genetic merits. There were no significant differences in the efficiency of the GS based on BLUP (RR-BLUP and GBLUP), the most common statistical approach. The increase of MM data, make GS efficiency do not vary widely.

Key words: Systematic review; Random effects model; Forest plot; Predictive accuracy.

---

 

INTRODUCCIÓN

La selección genómica (SG) es una técnica con alto potencial para acelerar la tasa de ganancia genética en vegetales (Heffner et al., 2009). Valiéndose de modelos estadísticos, permite relacionar vasta cantidad de marcadores moleculares (MM) o información genómica a un carácter fenotípico de interés, para predecir luego el mérito genético de cada fenotipo. En SG se parte de una población de entrenamiento o calibración, donde no sólo el genotipo molecular es conocido sino también el fenotipo, y se estiman modelos relacionales, que aprendiendo desde dicha población son luego aplicados a poblaciones de líneas donde no se conoce el fenotipo pero si se desea predecir el mérito genético. Es a partir del modelo estadístico estimado o ajustado que se realizan predicciones para estimar el valor de cría o mérito genético de cada individuo en la población de interés. Así, es posible seleccionar individuos con características promisorias para un determinado carácter, usando sólo la información molecular que usualmente proviene del genotipado con marcadores moleculares distribuidos en todo el genoma de cada individuo (Hawkins y Yu, 2018). La información del genotipo y del fenotipo en la población de entrenamiento también es usada para estimar el efecto de cada marcador sobre el carácter de interés. Aun con gran cantidad de MM, los modelos estadísticos usados en SG permiten ajustar el efecto de todos los marcadores simultáneamente. Si los MM se encuentran en desequilibrio de ligamiento con la mutación que afecta el carácter, los marcadores serán capaces de capturar una gran proporción de la varianza genética del carácter de interés (Voss Fels et al., 2019) y el modelo estadístico permitirá asociar los MM con el fenotipo (Hawkins y Yu, 2018). El modelo aplicado sobre la población de mejora se usa para predecir el valor genético del individuo desde la información molecular distribuida en todo el genoma (Genome Estimated Breeding Value-GEBV) (Bhat et al., 2016; Hawkins y Yu, 2018). La SG tiene la capacidad de utilizar altas cantidades de MM asociados a cada loci, incluso de efecto menor (Heffner et al., 2009) y así capturar mayor variación genética.
La eficiencia de la SG en un contexto particular, puede evaluarse a través de las correlaciones entre los fenotipos observados y los méritos genéticos predichos o valor de cría (GEBV). Existen una importante cantidad de estudios primarios de SG en vegetales, y si bien es posible su recopilación a través de la revisión sistemática de literatura, no es común encontrar estudios secundarios o meta-análisis (MA) de esos estudios primarios. La revisión sistemática permite sintetizar la información científica disponible, pero es el MA la técnica que permite incrementar la potencialidad de las conclusiones de los estudios primarios (Ferreira González et al., 2011).
La revisión sistemática involucra una serie de acciones: i) formular la pregunta de investigación a partir de la cual se realiza un constructo de búsqueda para explorar plataformas digitales; ii) realizar la búsqueda de manera exhaustiva y comprensiva de estudios primarios en diferentes bases de datos; iii) compactar la información obtenida de las diferentes bases de datos a través de un gestor bibliográfico; iv) establecer los criterios de exclusión e inclusión para la selección de estudios primarios; v) determinar la relevancia de los estudios identificados; y vi) extraer los datos en el formato necesario para el MA que se quiera realizar (Pai et al., 2004; Akobeng, 2005; Borenstein et al., 2009; 2010; Sánchez Meca, 2010). El término MA fue introducido por primera vez por Glass (1976), para denotar la síntesis estadística de los resultados de estudios primarios similares respecto al tema objeto de estudio. El MA permite: i) sintetizar los resultados de estudios primarios obtenidos de la revisión sistemática para incrementar la potencia de las pruebas de hipótesis de interés; ii) estimar el tamaño del efecto de interés o efecto global; iii) evaluar heterogeneidad entre estudios; y iv) en caso de que sea necesario, hacer análisis por subgrupos o meta-regresiones para comprender el impacto de factores y covariables sobre el tamaño del efecto en cada estudio primario (Borenstein et al., 2009). El MA permite estimar un efecto global o de síntesis de los estudios primarios. En este trabajo, el efecto que se midió a través del MA de estudios de SG es el tamaño o magnitud de la correlación entre valores fenotípicos observados y méritos genéticos predichos por los modelos de SG en las poblaciones de mejora. El gráfico Forest Plot, permite visualizar los resultados del MA a través de intervalos de confianza para el valor esperado del efecto de interés, tanto para cada estudio primario como para el conjunto de éstos. La amplitud de estos intervalos de confianza dependerá de la precisión con que se reportan los resultados de cada estudio primario; ésta es función del tamaño muestral y de la varianza residual. El efecto global es estimado como una media ponderada de los efectos reportados en los estudios primarios, y esta ponderación depende de la precisión de cada estudio. En escenarios de alta heterogeneidad entre estudios respecto al tamaño del efecto objeto de estudio, se realizan análisis por subgrupos de estudios primarios relativamente homogéneos. En los estudios de SG en vegetales, es frecuente que se presenten datos de otras variables que podrían marcar diferencias o generar heterogeneidad entre estudios, como por ejemplo, la cantidad de genotipos evaluados, la cantidad de marcadores moleculares empleados (Wu y Hu, 2012) o los modelos estadísticos usados para la SG. Esta información puede ser considerada para conformar subgrupos para el MA y así comparar el impacto de los distintos niveles de estos factores sobre la correlación objeto de estudio. El objetivo de este trabajo fue realizar un MA de la eficiencia de la SG en cereales y su dependencia con la cantidad de MM y el modelo estadístico usado.

MATERIALES Y MÉTODOS

Recolección de la información a través de la revisión sistemática
En la revisión sistemática se seleccionaron palabras clave relacionadas a la pregunta de investigación, y de este compendio de palabras se construyó el siguiente constructo de búsqueda: (GS o “Genomic Selection”) y (“Plant breeding”) y (crops) para obtener la mayor cantidad posible de literatura referente a estudios de SG en mejoramiento vegetal. La búsqueda de estudios primarios fue llevada a cabo en múltiples bases de datos: Scopus, Science Direct, EBSCOhost, Pubmed, JSTOR, Red de Revistas Científicas de América Latina y el Caribe, España y Portugal “Redalyc” y SpringerLink. Se obtuvieron 5014 estudios primarios que mencionaran la SG en vegetales. A través del gestor bibliográfico Zotero se realizó la unificación de los estudios primarios obtenidos en las siete bases de datos electrónicas, así como la eliminación de estudios primarios duplicados, excluyendo 779 estudios primarios. Luego, se seleccionaron aquellos estudios que contenían las palabras de búsqueda en el título (947 estudios primarios). Seguidamente, se leyeron los resúmenes de los trabajos que pasaron el filtrado del título y se eligieron aquellos que tratasen la eficiencia de la SG (se desecharon otros 358 estudios primarios). Los estudios que pasaron la anterior etapa (589 trabajos), fueron leídos de manera completa para seleccionar aquellos estudios donde estaba publicada la información necesaria para la construcción de la base de datos (especies, carácter fenotípico, cantidad de marcadores, métodos de estimación y la precisión de la predicción (prediction accuracy), medida a través del coeficiente de correlación “r” entre el fenotipo observado y los valores de mejora predichos. Finalmente, la cantidad de estudios primarios seleccionados para la conformación de la base de datos fue de 68. En la Figura 1 se presenta un diagrama de flujo de los pasos mencionados.

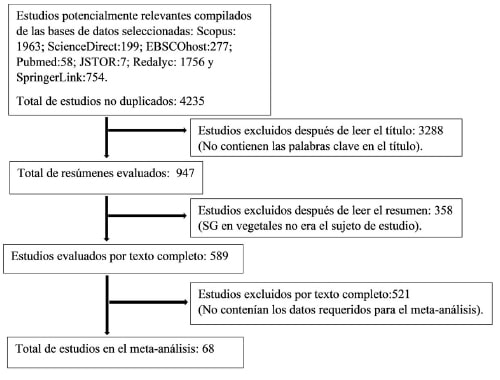
Figura 1. Diagrama de flujo de los criterios de exclusión para el meta-análisis.

Conformación de la base de datos para realizar el metaanálisis
La base de datos quedó conformada por 68 estudios primarios, aunque en algunos de ellos se evaluaron varios casos, i.e., más de un proceso de SG y por tanto se pudieron obtener varios coeficientes de correlación, totalizando 232 casos de SG. La base de datos conformada a partir de los estudios primarios seleccionados contiene la variable “Estudios” para identificar los estudios primariosa través de sus autores y el año de la publicación. Una columna denominada “Subgrupo_Especies” con dos categorías: “cereales” (trigo, maíz, cebada, arroz y centeno) y “otras especies” (césped, soja, colza, remolacha, alfalfa, eucalipto, pera, raigrás, mandioca, caña de azúcar y vid). Para este trabajo se consideraron los datos provenientes de SG en cereales. La columna “carácter” recopila la variable fenotípica analizada en la población de entrenamiento (rendimiento de grano, tiempo de floración, altura de planta, contenido de proteína). La columna “Total_Marcadores” contiene la cantidad de marcadores moleculares usados en cada estudio primario y categorizada en terciles de la distribución de cantidad de marcadores: baja≤1.700, media=(1.700; 17.000] y alta>17.000. La columna “Método_Estimación”, reporta los métodos de estimación usados en la SG que luego son reagrupados en dos categorías: “basados en BLUP” (BLUP, G-BLUP y RR-BLUP) y “otros”, que incluyen “métodos bayesianos o de aprendizaje automático” (M-BL, SVR, RKHS, Bayes A y Bayes B). La última columna contiene el coeficiente de correlación “r” entre el fenotipo observado y el mérito genético predicho por SG reportado en cada estudio primario. Un valor de correlación cercano a uno indica alta eficiencia de la SG. Los métodos basados en modelos mixtos y consecuentemente en el mejor predictor lineal insesgado (BLUP) han sido los más usados en SG.
El método G-BLUP se caracteriza por asignar la misma varianza a todos los loci, es decir, otorga la misma importancia a cada alelo del marcador para obtener el predictor del mérito genético, i.e., como suma los efectos alélicos individuales; algunos marcadores pueden asociarse a efectos nulos (Clark y van derWerf, 2013). Por otra parte, el método RR-BLUP asume que todos los loci tienen el mismo efecto, distinto de cero con las mismas varianzas, pero esto no implica que todos los MM tengan el mismo efecto. RR-BLUP estima la matriz de relaciones entre los genotipos a partir de la información provista por los MM, por lo tanto, algunos loci pueden aportar al predictor y otros no. Los métodos bayesianos ponderan el efecto de cada locus con distinta varianza a diferencia de RR-BLUP. Entre los métodos basados en aprendizaje automáticos, SVM ha sido uno de los más usados en la SG, dado que al usar una función kernel para los cálculos como el producto interno, resuelve el problema de estimación con alta dimensionalidad. Por ello, en estos tipos de modelos, la selección de la función kernel se vuelve un factor clave, dado que la misma debe reflejar la distribución característica de la muestra de entrenamiento (Wang et al., 2018).

Meta-análisis
Se estimó la correlación (promedio ponderado de los estudios) entre los valores observados y predichos por el modelo en los estudios de SG realizados en maíz y trigo; especies que representaron más del 50% del total de casos detectados en la revisión sistemática. Se usó un modelo de efectos aleatorios para el MA, ya que se observó alta heterogeneidad entre estudios respecto a los valores de r y la precisión reportada:

donde ri es la correlación observada, μ es la correlación esperada entre el fenotipo observado y el mérito genético predicho, τi es un efecto aleatorio asociado a cada estudio primario que se supone con distribución N(0,τ) y i es un término de error aleatorio con distribución N(0,σ2) que mide la precisión dentro de cada caso de SG.
La heterogeneidad entre estudios se evaluó con el estadístico I2, que permite cuantificar cuánto de la variabilidad total en el estadístico de interés debe ser atribuida a la variación entre estudios (Higgins et al., 2003). Es una medida independiente del número de estudios incluidos en el meta-análisis y de la unidad de medida utilizada para cuantificar el efecto estudiado. El estadístico I2, se expresa como una proporción, un valor cercano a cero indica que la varianza observada es espuria y por lo tanto, los estudios primarios pueden considerarse homogéneos. Higgins et al. (2003) sugirieron que valores de I2 hasta 25% podrían ser indicadores de baja heterogeneidad, entre 25 y 50% de mediana heterogeneidad y más de 75% de alta heterogeneidad. Dado los altos valores encontrados para I2, se llevaron a cabo análisis por subgrupos considerando en cada análisis diferentes variables de clasificación, como la cantidad de marcadores moleculares utilizados (“Subgrupo_MM”) y el tipo de método de estimación utilizado para la SG (variable “Método_Estimación”). La estrategia de realizar análisis por subgrupo, además de controlar la heterogeneidad entre estudios, permitió detectar cómo estás variables contribuyen en la estimación global de la eficiencia de la SG. Los metaanálisis se realizaron con los datos transformados a través del z de Fisher, pero los resultados de los efectos globales fueron reportados en la métrica de correlaciones. Los datos fueron analizados usando el software R con el paquete meta (R Core Team 2020).

RESULTADOS

La SG en cereales ha convocado mayor atención que en otras especies agrícolas por el acortamiento aparejado en el ciclo de mejoramiento genético vegetal. Probablemente, este hecho se asocie con la importancia alimentaria de estas especies agrícolas que cuentan con programas de mejoramiento genético vegetal en gran parte del mundo.
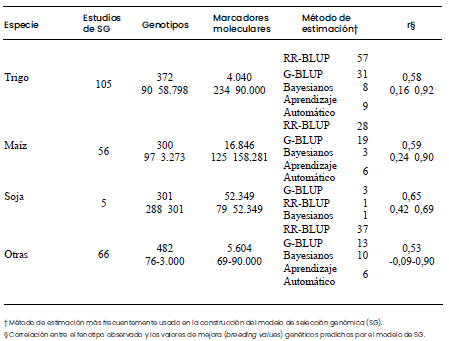
Los resultados reportados en la Tabla 1 indican predominancia del uso de los métodos de estimación RR-BLUP y G-BLUP en el ajuste del modelo estadístico que permitirá obtener las predicciones para la SG. Es importante destacar que se observó alta variabilidad en los reportes de eficiencia de la SG; por ejemplo, en trigo algunas publicaciones reportaban correlaciones menores al 20% mientras que otras reportaban valores de correlaciones en el valor fenotípico observado y el valor genético predicho mayores al 80%. No obstante, en la mayoría de los casos analizados la eficiencia de la SG fue cercana al 60%, que en términos estadísticos es mediana, pero en términos prácticos puede ser suficiente.

Tabla 1. Estudios de selección genómica (SG) en cultivos (n=232) según especie, cantidad de genotipos y de marcadores moleculares en la población de entrenamiento, método de estimación y eficiencia promedio.

La representación gráfica de los resultados se realiza con un Forest Plot (Figura 2), cuyas filas representan cada uno de los estudios primarios y la eficiencia de la SG en las especies trigo y maíz agrupadas según el método de estimación del modelo de SG (G-BLUP y RR-BLUP). El tamaño del efecto es la magnitud de la asociación entre el valor fenotípico observado y el valor genético predicho. Así, el gráfico permite visualizar la correlación de interés promedio (cuadrado) de cada estudio primario y su intervalo de confianza (IC) con nivel de confianza del 95%. Mientras menor es la amplitud del intervalo de confianza, mayor es la precisión en la estimación del coeficiente de correlación entre el valor fenotípico observado y el valor genético predicho. El cuadrado que representa el tamaño del efecto de cada estudio primario varía entre estudios para reflejar el peso de cada uno en la estimación del efecto global (correlación promedio ponderada). Un estudio con precisión relativamente buena, tendrá asignada mayor ponderación o peso para generar la estimación global. La precisión está gobernada por el tamaño de la muestra y por la varianza residual del estudio. Al final de la lista de estudios se visualiza el efecto global (rombo). Si la correlación global es estadísticamente distinta de cero, el valor de cría predicho por el modelo se correlaciona con el valor observado y la SG es eficiente. El efecto global de la correlación entre los valores observados y los valores predichos fue de 0,61, con un intervalo de confianza (IC) de [0,59-0,64] que confirma la eficiencia de la SG. La heterogeneidad entre estudios fue alta I2=99% y estadísticamente significativa p<0,001; como estrategia analítica para controlar parte de la heterogeneidad, se identificaron subgrupos relacionados al método de estimación (Figura 2) y a la cantidad de marcadores moleculares involucrados en la construcción del modelo de SG (Figura 3).

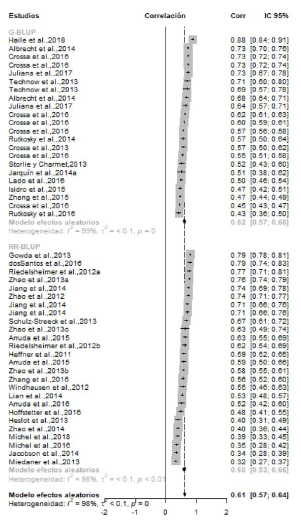
Figura 2. Forest Plot de la eficiencia de SG para los métodos de estimación G-BLUP y RR-BLUP en trigo y maíz. El modelo de metaanálisis ajustado fue un modelo de efectos aleatorios por subgrupos (G-BLUP y RR-BLUP), contemplando de esta forma la heterogeneidad entre estudios primarios y entre grupos. Las correlaciones se presentan ordenadas de mayor a menor dentro de cada método de estimación.

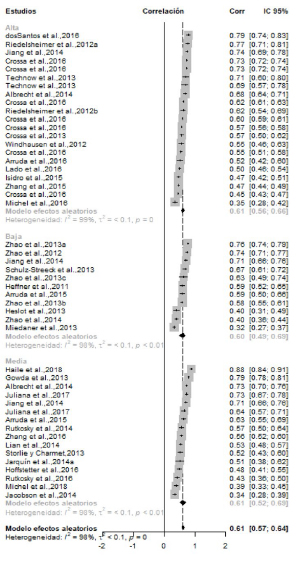
Figura 3. Forest Plot de la eficiencia de SG para distintas densidades de marcadores moleculares categorizadas en: baja (menos de 1.700), media (entre 1.700 y 17.000) y alta densidad de marcadores moleculares, mayor a 17.000 para estudios primarios de trigo y maíz. El modelo de meta-análisis ajustado fue un modelo de efectos aleatorios por subgrupos de densidad de marcadores moleculares (Alta, Baja y Media), contemplando de esta forma la heterogeneidad entre estudios primarios y entre grupos. Las correlaciones se presentan ordenadas de mayor a menor dentro de cada categoría de densidad de marcadores moleculares.

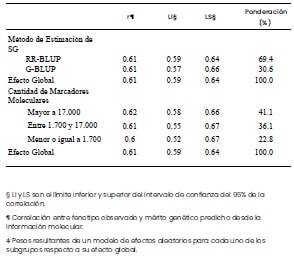
El intervalo de confianza (IC) para G-BLUP fue [0,57- 0,66] y para RR-BLUP [0,59-0,64]; en ambos casos no contienen al cero e indican que la eficiencia de la SG es similar entre ellos y que no estuvo condicionada por la selección de uno u otros métodos de estimación basados en BLUP. La superposición de los IC indica que no existen diferencias estadísticamente significativas entre ambos métodos de construcción del modelo para predecir mérito genético desde la información genómica. Los resultados del meta-análisis para trigo y maíz, realizado por subgrupos definidos por la densidad de marcadores moleculares (alta con más de 17.000 MM, media de 1.700 hasta 17.000 MM y baja con 1.700 o menos MM), mostraron similitud de la eficiencia alcanzada con distinta cantidad de marcadores moleculares (cerca del 60%) (Figura 3). Las ponderaciones o pesos reportados para las categorías alta y media fueron 41,1% y 36,1% respectivamente, mientras que las ponderaciones de la categoría de baja densidad de marcadores moleculares fue de 22,8%. Esto evidenció que la mayor contribución al efecto global de correlación entre los valores observados y predichos, se obtuvieron con densidades de marcadores moleculares medias y altas (Tabla 2).

Tabla 2. Estimación de la correlación entre fenotipo observado y mérito genético predicho desde la información molecular de los métodos de estimación más frecuentes de selección genómica y densidad de marcadores moleculares en maíz y trigo (n=122).

DISCUSIÓN

La SG se comenzó a aplicar para la predicción genética en animales (Meuwissen et al., 2001), no obstante, fue adaptada rápidamente en los programas de mejoramiento genético vegetal (Thavamanikumar et al., 2015). Se presenta como una herramienta que permite predecir de manera efectiva, los méritos genéticos de los individuos a partir de información genómica, sin necesidad de observar el fenotipo; así la selección se puede realizar de manera más rápida.
Diferentes modelos estadísticos son usados para asociar la variabilidad genómica a un carácter fenotípico de interés y poder luego predecir el mérito genético de un nuevo individuo. Sin embargo, han manifestado la complejidad a la hora de comparar los resultados de diferentes estudios, además consideran que no siempre se ajusta el modelo más eficiente para un estudio en particular (Wang et al., 2015). Los resultados del metaanálisis conducido en este trabajo, sugieren que no existe una diferencia significativa entre el ajuste del modelo por G-BLUP o RR-BLUP, dos de los métodos más usados para la construcción del modelo de SG.
Dado que los valores de correlación dependen fuertemente de las varianzas de las variables que se correlacionan, y que éstas pueden ser distintas bajo distintos escenarios, el meta-análisis se realizó previa transformación (z de Fisher) de las correlaciones reportadas. La transformación del coeficiente de correlación en la escala z de Fisher permite realizar el meta-análisis en una escala común y luego transformar el tamaño del efecto y los intervalos de confianza logrados a las escalas originales (Borenstein et al., 2009). Algunos autores sugieren que la transformación z de Fisher podría producir un sesgo hacia la derecha (Silver y Dunlap, 1987; Strube, 1988; Field, 2001; 2005). Otros autores sugieren que la transformación logra que el error estándar y, por lo tanto los intervalos de confianza, dependan únicamente del tamaño muestral y no del tamaño de la correlación observada, que puede verse afectada por el error de muestreo (Silver y Dunlap, 1987; Field, 2005). Strube (1988) señaló que a medida que aumenta el número de estudios primarios, el sesgo debido a la transformacion es despreciable. En nuestro trabajo el número de correlaciones derivadas de los estudios primarios fue alto (n=232 cuando se trabajó con todos los casos y n=48 cuando se analizaron las medias de correlaciones por publicación). Mas allá de la existencia de un posible sesgo, las correlaciones promedio, aunque significativas, no fueron altas (aprox. r=0,6) sugiriendo que existe espacio para mejorar la capacidad predictiva de los modelos usados en SG en trigo y maíz.
Podría ser importante considerar efectos de interacción entre los efectos de marcadores en los modelos lineales usados para SG con el fin de incrementar la eficiencia de la SG. Conceptualmente estos modelos son entendibles, pero son computacionalmente difíciles de estimar en la actualidad. Los métodos de base computacional como algunos modelos de regresión de aprendizaje automático podrían ofrecer una herramienta para el tratamiento de interacciones de orden múltiple. Varios métodos de ajustes de modelos de SG abordan los problemas de la alta dimensionalidad y la complejidad computacional capturando diferentes aspectos de la asociación entre el genotipo y el fenotipo. Sin embargo, el desempeño de diferentes métodos depende de la arquitectura genética subyacente del carácter de interés (Resende et al., 2012; Wang et al., 2018). Se ha discutido en la literatura que la precisión de la SG depende de la heredabilidad y de la distribución de los genes causales (Desta y Ortiz, 2014) y consecuentemente la heredabilidad del carácter en estudio se relaciona positivamente a la precisión de la predicción. Otro factor importante que debe ser considerado es la interacción genotipo-ambiente (G×E); ya que predicciones sobre el mismo carácter, pero evaluados en varios ambientes, difieren considerablemente debido al efecto que causa esta interacción (Wang et al., 2018). Su et al. (2012) usaron predicción genómica con densidades extremas de SNPs y observaron que cuando aumentaron la cantidad de información genómica en un 1438%, la precisión de la predicción aumentó solo en 0,5-1,0%. Aun cuando se conoce que cuanto más marcadores haya mejor será la predicción, la precisión es difícil de mejorar significativamente cuando la densidad inicial de marcadores ya es alta. Los resultados del meta-análisis son consistentes con estas publicaciones. Nakaya e Isobe (2012) realizaron otra revisión de estudios donde se estimaba el mérito genético sobre bases de datos simulados y bases de datos reales, y reportaron que la predicción del valor de cría fue siempre mejor cuando en los modelos se incorporó información provista por marcadores moleculares distribuidos densamente en el genoma respecto a los modelos tradicionales de la construcción del BLUP solo con datos fenotípicos. En otros estudios para caracteres relacionados a calidad de grano en poblaciones biparentales de trigo, se observó que la precisión de los modelos de SG alcanzó una meseta con una densidad de marcadores moleculares que se acercaba a los 256 (Heffner et al., 2011). Para otras especies, como pinos, se observó que la máxima capacidad predictiva se alcanzó en subconjuntos de 564 marcadores moleculares y luego disminuyó (Resende et al., 2012). El mismo fenómeno se observó en otro estudio pero con una densidad de marcadores mucho mayor, ya que se usaron 3490 marcadores moleculares para calibrar los modelos de SG (Oakey et al., 2016). Yang et al. (2010) y Wang et al. (2017) concluyeron que cuando la densidad de marcadores alcanza un cierto nivel, la predicción genómica no se beneficia.
Entre los métodos estadísticos para ajustar el modelo de SG, el más recomendado en la práctica de mejoramiento, debido a su robustez y eficiencia computacional es el G-BLUP (Wang et al., 2018). No obstante, algunos algoritmos de aprendizaje de máquinas, como RKHS (Reproducing Kernel Hilbert Space) han tomado un papel muy importante en SG (Cuevas et al., 2016). El método G-BLUP asume que todos los efectos de marcador se distribuyen normalmente con igual varianza (Meuwissen et al., 2001) y puede producir resultados similares al método Bayes C (Ferrão et al., 2017). En el trabajo de Gianola (2013) se aprecia que el método de G-BLUP es similar al RR-BLUP, como también se observó en el meta-análisis de este trabajo. Daetwyler et al. (2014) calibraron modelos de SG basados en G-BLUP y en regresión bayesiana para predecir la resistencia a la roya en trigo, y concluyeron que el modelo G-BLUP presentó mejor desempeño que la regresión bayesiana. En trigo, los modelos de SG bayesianos han mostrado resultados prometedores en el contexto del análisis de QTL (quantitative trait loci), siendo más sensibles al aumento del número de QTL sin disminuir la precisión en contextos de múltiples QTL (Wang et al., 2015).
La precisión que aportan los métodos G-BLUP y RR-BLUP se puede mantener casi constante, independientemente de la cantidad de QTL (Wang et al., 2018). Si bien los modelos Bayes A y Bayes B han mostrado buen desempeño (De los Campos et al., 2009) la estimación de los modelos bayesianos puede llevar mucho tiempo restringiendo su aplicación. Friedman et al. (2010) mostraron una mejor alternativa con el algoritmo LASSO, que logra un equilibrio entre la contracción selectiva de los efectos alélicos y la eficiencia computacional. A pesar del buen desempeño de los modelos bayesianos en SG animal (Neves et al., 2014), Xu et al. (2017) señalaron que el modelo G-BLUP tiene mejor desempeño que los bayesianos en la predicción de caracteres relacionados con el rendimiento en maíz y también, en la predicción del rendimiento en grano de trigo. En el presente trabajo se observó que la eficiencia de la SG no difiere significativamente entre el uso de G-BLUP o RR-BLUP para el ajuste del modelo, resultado consistente con lo publicado (Dong et al., 2016; Ferrão et al., 2017).
En conclusión, aún cuando los modelos estadísticos usados para SG en cultivos de importancia agrícola han contribuido en la predicción genómica, permitiendo seleccionar genotipos promisorios en etapas tempranas de los programas de mejoramiento genético vegetal, aún es necesario incrementar la capacidad predictiva. Los modelos más usados en maíz y trigo para predecir mérito genético han sido G-BLUP y RR-BLUP, sin diferencias estadísticas en su performance. Si bien la capacidad predictiva aumenta con el número de marcadores usados, la respuesta no es lineal y en algunas situaciones el incremento de estos podría no ser redituable en términos del aumento producido sobre la eficiencia de la SG.

BIBLIOGRAFÍA

1. Akobeng A.K. (2005) Understanding systematic reviews and metaanalysis. Archives of Disease in Childhood 90 (8): 845-848.

2. Bhat J.A., Ali S., Salgotra R.K., Mir Z.A., Dutta S., Jadon V., Tyagi A., Mushtaq M., Jain N., Singh P.K., Singh G.P., Prabhu K.V. (2016) Genomic selection in the era of next generation sequencing for complex traits in plant breeding. Frontiers in Genetics 7: 221.

3. Borenstein M., Hedges L.V., Higgins J.P.T., Rothstein H.R. (2009) Introduction to meta-analysis. John Wiley & Sons. Ltd., Chichester, UK.

4. Borenstein M., Hedges L.V., Higgins J.P.T., Rothstein H.R. (2010) A basic introduction to fixed-effect and random-effects models for metaanalysis. Research Synthesis Methods 1 (2): 97-111.

5. Clark S.A., van der Werf J. (2013) Genomic best linear unbiased prediction (gBLUP) for the estimation of genomic breeding values. In: Gondro C., van der Werf J., Hayes B. (Eds.) Genome-Wide Association Studies and Genomic Prediction. Springer Protocols, pp. 321-330.

6. Cuevas J., Crossa J., Soberanis V., Pérez Elizalde S., Pérez Rodríguez P., de los Campos G., Montesinos López O.A., Burgueño J. (2016) Genomic prediction of genotype × environment interaction kernel regression models. The Plant Genome 9 (3).

7. Daetwyler H.D., Bansal U.K., Bariana H.S., Hayden M.J., Hayes B.J. (2014) Genomic prediction for rust resistance in diverse wheat landraces. Theoretical and Applied Genetics 127 (8): 1795-1803.

8. de los Campos G., Naya H., Gianola D., Crossa J., Legarra A., Manfredi E., Weigel K., Cotes J.M. (2009) Predicting quantitative traits with regression models for dense molecular markers and pedigree. Genetics 182 (1): 375-85.

9. Desta Z.A., Ortiz R. (2014) Genomic selection: genome-wide prediction in plant improvement. Trends in Plant Science 19 (9): 592-601.

10. Dong L., Xiao S., Wang Q., Wang Z. (2016) Comparative analysis of the GBLUP, emBayesB, and GWAS algorithms to predict genetic values in large yellow croaker (Larimichthys crocea). BMC Genomics 17 (1): 460.

11. Ferrão L.F.V., Ortiz R., Garcia A.A.F. (2017) Genomic selection: state of the art. In: Campos H., Caligari P. (Eds.) Genetic Improvement of Tropical Crops. Springer, pp. 19-54.

12. Ferreira González I., Urrútia G., Alonso Coello P. (2011) Revisiones sistemáticas y metaanálisis: bases conceptuales e interpretación. Revista Española de Cardiología 64 (8): 688-696.

13. Field A.P. (2001) Meta-analysis of correlation coefficients: a Monte Carlo comparison of fixed- and random-effects methods. Psychological Methods 6 (2): 161-180.

14. Field A.P. (2005) Is the meta-analysis of correlation coefficients accurate when population correlations vary? Psychological Methods 10 (4): 444-467.

15. Friedman J., Hastie T., Tibshirani R. (2010) Regularization Paths for Generalized Linear Models via Coordinate Descent. Journal of Statistical Software 33 (1): 1-22.

16. Gianola D. (2013) Priors in whole-genome regression: the Bayesian alphabet returns. Genetics 194 (3): 573-596.

17. Glass G.V. (1976) Primary, secondary, and meta-analysis of research. Educational Researcher 5 (10): 3-8.

18. Hawkins C., Yu L.X. (2018) Recent progress in alfalfa (Medicago sativa L.) genomics and genomic selection. The Crop Journal 6 (6): 565-575.

19. Heffner E.L., Jannink J.L., Iwata H., Souza E., Sorrells M.E. (2011) Genomic selection accuracy for grain quality traits in biparental wheat populations. Crop Science 51: 2597- 2606.

20. Heffner E.L., Sorrells M.E., Jannink J.L. (2009) Genomic selection for crop improvement. Crop Science 49 (1): 1-12.

21. Higgins J.P.T., Thompson S.G, Deeks J.J., Altman D.G. (2003) Measuring inconsistency in meta-analyses. BMJ 327 (7414): 557-560.

22. Meuwissen T.H., Hayes B.J., Goddard M.E. (2001) Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 157 (4): 1819-1829.

23. Nakaya A., Isobe S.N. (2012) Will genomic selection be a practical method for plant breeding? Annals of Botany 110 (6): 1303- 1316.

24. Neves H.H.R., Carvalheiro R., O’Brien A.M.P., Utsunomiya Y.T, do Carmo A.S, Schenkel F.S, Sölkner J., McEwan J.C., Van Tassell C.P., Cole J.B., da Silva M.V.G.B., Queiroz S.A., Sonstegard T.S., Garcia J.F. (2014) Accuracy of genomic predictions in Bos indicus (Nellore) cattle. Genetics Selection Evolution 46 (1): 17.

25. Oakey H., Cullis B., Thompson R., Comadran J., Halpin C., Waugh R. (2016) Genomic selection in multi-environment crop trials. G3: Genes, Genomes, Genetics 6 (5): 1313- 1326.

26. Pai M., McCulloch M., Gorman J.D., Pai N., Enanoria W., Kennedy G., Tharyan P., Colford J.M. (2004) Systematic reviews and meta-analyses: an illustrated, step-by-step guide. The National Medical Journal of India 17 (2): 86-95.

27. R Core Team (2020) R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna.

28. Resende M.F.R., Muñoz P., Resende M.D.V., Garrick D.J., Fernando R.L., Davis J.M., Jokela E.J., Martin T.A., Peter G.F., Kirst M. (2012) Accuracy of genomic selection methods in a standard data set of Loblolly Pine (Pinus taeda L.). Genetics 190 (4): 1503-1510.

29. Sánchez Meca J. (2010) Cómo realizar una revisión sistemática y un meta-análisis. Aula Abierta 38 (2): 53-64.

30. Silver N.C., Dunlap W.P. (1987) Averaging correlation coefficients: should Fisher’s z transformation be used? Journal of Applied Psychology 72 (1): 146-148.

31. Strube M.J. (1988) Averaging correlation coefficients: influence of heterogeneity and set size. Journal of Applied Psychology 73 (3): 559-568.

32. Su G., Brøndum R.F., Ma P., Guldbrandtsen B., Aamand G.P., Lund M.S. (2012) Comparison of genomic predictions using mediumdensity (~54,000) and high-density (~777,000) single nucleotide polymorphism marker panels in Nordic Holstein and Red Dairy Cattle populations. Journal of Dairy Science 95 (8): 4657-4665.

33. Thavamanikumar S., Dolferus R., Thumma B.R. (2015) Comparison of genomic selection models to predict flowering time and spike grain number in two hexaploid wheat doubled haploid populations. G3: Genes, Genomes, Genetics 5 (10): 1991-1998.

34. Voss Fels K.P., Cooper M., Hayes B.J. (2019) Accelerating crop genetic gains with genomic selection. Theoretical and Applied Genetics 132 (3): 669-686.

35. Wang X., Li L., Yang Z., Zheng X., Yu S., Xu C., Hu Z. (2017) Predicting rice hybrid performance using univariate and multivariate GBLUP models based on North Carolina mating design II. Heredity 118: 302-310.

36. Wang X., Xu Y., Hu Z., Xu C. (2018) Genomic selection methods for crop improvement: Current status and prospects. The Crop Journal 6 (4): 330-340.

37. Wang X., Yang Z., Xu C. (2015) A comparison of genomic selection methods for breeding value prediction. Science Bulletin 60 (10): 925-935.

38. Wu X.L., Hu Z.L. (2012) Meta-analysis of QTL mapping experiments. In: Rifkin S.A. (Ed.) Quantitative Trait Loci (QTL): Methods and Protocols. Totowa, NJ, Humana Press, pp. 145-171.

39. Xu Y., Xu C., Xu S. (2017) Prediction and association mapping of agronomic traits in maize using multiple omic data. Heredity 119 (3): 174-184.

40. Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R., Madden P.A., Heath A.C., Martin N.G., Montgomery G.W., Goddard M.E., Visscher P.M. (2010) Common SNPs explain a large proportion of the heritability for human height. Nature Genetics 42: 565-569.